Getting Started#
We’re going to demonstrate how to estimate recruitment curves using a hierarchical Bayesian model and the rectified-logistic function.
A Simple Example#
Tip
If you have trouble running the commands in this tutorial, please copy the command and its output, then open an issue on our GitHub repository. We’ll do our best to help you!
Begin by reading the mock_data.csv file:
import pandas as pd
url = "https://raw.githubusercontent.com/hbmep/hbmep/refs/heads/docs-data/data/mock_data.csv"
df = pd.read_csv(url)
df shape: (245, 4)
df columns: TMSIntensity, participant, PKPK_ECR, PKPK_FCR
All participants: P1, P2, P3
First 5 rows:
TMSIntensity participant PKPK_ECR PKPK_FCR
0 43.79 P1 0.197 0.048
1 55.00 P1 0.224 0.068
2 41.00 P1 0.112 0.110
3 43.00 P1 0.149 0.058
4 14.00 P1 0.014 0.011
This dataset contains TMS responses (peak-to-peak amplitude, in mV) for three participants (P1, P2, P3), recorded from two muscles (ECR and FCR).
The column TMSIntensity represents stimulation intensity in percent maximum stimulator output (0–100% MSO).
Build the model#
Next, we initialize a standard hierarchical Bayesian model. This step typically consists of assigning the model’s attributes to the appropriate dataframe columns, setting the sampling parameters, and choosing the recruitment curve function.
from hbmep.model.standard import HB
model = HB()
# Point to the respective columns in dataframe
model.intensity = "TMSIntensity"
model.features = ["participant"]
model.response = ["PKPK_ECR", "PKPK_FCR"]
# Specify the sampling parameters
model.mcmc_params = {
"num_chains": 4,
"thinning": 1,
"num_warmup": 1000,
"num_samples": 1000,
}
# Set the function
model._model = model.rectified_logistic
Alternatively, these settings can be specified in an hbmep.toml configuration file without having to change the code directly. See Working with TOML configuration file for details.
Running the model#
Before fitting the model, we can visualize the dataset. Since the plot is saved as a PDF, we need to specify an output path.
import os
current_directory = os.getcwd()
output_path = os.path.join(current_directory, "dataset.pdf")
# Plot dataset and save it as a PDF
model.plot(df, output_path=output_path)
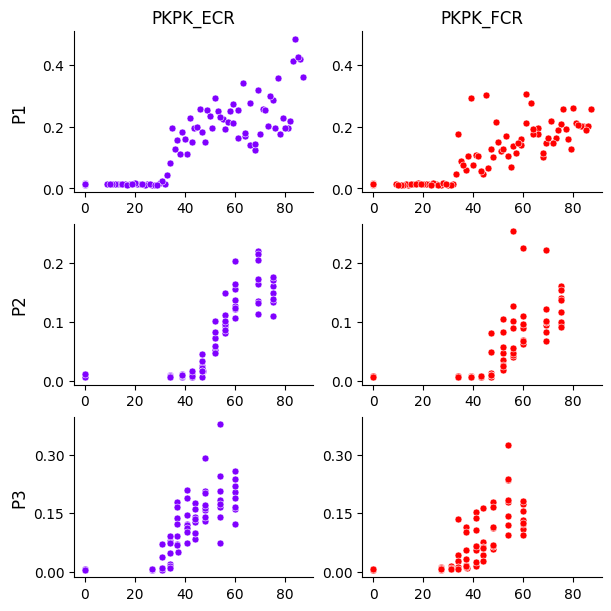
The plot shows rows as participants and columns as muscles. The x-axis is TMS intensity (% MSO), and the y-axis is MEP peak-to-peak amplitude (mV).
Next, we process the dataframe by encoding categorical feature columns. This returns the same dataframe with encoded values, plus an encoder dictionary for mapping back to original labels.
# Process the dataframe
df, encoder = model.load(df)
Encoded participants: 0, 1, 2
Participant mapping: 0 -> P1, 1 -> P2, 2 -> P3
Now we run the model to estimate curves.
# Run
mcmc, posterior = model.run(df=df)
# Check convergence diagnostics
summary_df = model.summary(posterior)
print(summary_df.to_string())
Show code cell output
WARNING:2025-09-10 13:37:55,646:jax._src.xla_bridge:864: An NVIDIA GPU may be present on this machine, but a CUDA-enabled jaxlib is not installed. Falling back to cpu.
Compiling.. : 0%| | 0/2000 [00:00<?, ?it/s]
Running chain 0: 0%| | 0/2000 [00:02<?, ?it/s]
Running chain 0: 5%|▌ | 100/2000 [00:05<01:07, 28.04it/s]
Running chain 0: 10%|█ | 200/2000 [00:06<00:36, 49.70it/s]
Running chain 0: 15%|█▌ | 300/2000 [00:07<00:24, 70.24it/s]
Running chain 0: 20%|██ | 400/2000 [00:07<00:17, 93.04it/s]
Running chain 0: 25%|██▌ | 500/2000 [00:08<00:13, 107.38it/s]
Running chain 0: 30%|███ | 600/2000 [00:09<00:11, 125.25it/s]
Running chain 0: 35%|███▌ | 700/2000 [00:09<00:08, 146.29it/s]
Running chain 0: 40%|████ | 800/2000 [00:09<00:07, 166.56it/s]
Running chain 0: 45%|████▌ | 900/2000 [00:10<00:06, 182.06it/s]
Running chain 0: 50%|█████ | 1000/2000 [00:10<00:05, 192.61it/s]
Running chain 0: 55%|█████▌ | 1100/2000 [00:11<00:04, 193.64it/s]
Running chain 0: 60%|██████ | 1200/2000 [00:11<00:04, 186.25it/s]
Running chain 0: 65%|██████▌ | 1300/2000 [00:12<00:03, 183.70it/s]
Running chain 0: 70%|███████ | 1400/2000 [00:12<00:03, 185.69it/s]
Running chain 0: 75%|███████▌ | 1500/2000 [00:13<00:02, 178.36it/s]
Running chain 0: 80%|████████ | 1600/2000 [00:14<00:02, 176.14it/s]
Running chain 0: 85%|████████▌ | 1700/2000 [00:14<00:01, 178.43it/s]
Running chain 0: 90%|█████████ | 1800/2000 [00:15<00:01, 179.44it/s]
Running chain 3: 100%|██████████| 2000/2000 [00:15<00:00, 130.38it/s]
Running chain 2: 100%|██████████| 2000/2000 [00:15<00:00, 129.55it/s]
Running chain 1: 100%|██████████| 2000/2000 [00:15<00:00, 128.48it/s]
Running chain 0: 100%|██████████| 2000/2000 [00:16<00:00, 122.60it/s]
mean sd hdi_2.5% hdi_97.5% mcse_mean mcse_sd ess_bulk ess_tail r_hat
a_loc 35.418 5.576 24.891 47.705 0.157 0.299 2321.0 869.0 1.0
a_scale 11.170 7.101 3.772 25.594 0.231 0.376 1611.0 1203.0 1.0
b_scale 0.189 0.115 0.061 0.381 0.003 0.013 1563.0 1594.0 1.0
g_scale 0.013 0.005 0.006 0.024 0.000 0.000 1047.0 975.0 1.0
h_scale 0.282 0.129 0.120 0.524 0.004 0.007 1054.0 1250.0 1.0
v_scale 4.547 2.913 0.246 10.230 0.050 0.040 2554.0 1966.0 1.0
c₁_scale 3.008 2.633 0.075 8.490 0.051 0.045 2077.0 2303.0 1.0
c₂_scale 0.280 0.102 0.125 0.493 0.003 0.003 1194.0 1728.0 1.0
a[0, 0] 31.900 0.463 30.731 32.637 0.016 0.021 1815.0 754.0 1.0
a[0, 1] 31.609 0.538 30.537 32.577 0.011 0.010 2845.0 2277.0 1.0
a[1, 0] 45.521 0.870 43.650 46.427 0.034 0.069 1385.0 650.0 1.0
a[1, 1] 44.842 0.815 43.216 46.156 0.017 0.022 2870.0 2747.0 1.0
a[2, 0] 30.066 0.431 29.251 30.719 0.010 0.022 2563.0 1600.0 1.0
a[2, 1] 31.175 0.673 29.987 32.482 0.012 0.020 3614.0 2677.0 1.0
b_raw[0, 0] 1.118 0.479 0.330 2.112 0.011 0.007 1767.0 1753.0 1.0
b_raw[0, 1] 1.372 0.550 0.419 2.458 0.010 0.009 2899.0 2533.0 1.0
b_raw[1, 0] 0.607 0.356 0.078 1.335 0.010 0.009 1399.0 2050.0 1.0
b_raw[1, 1] 0.495 0.312 0.040 1.110 0.006 0.006 1912.0 2230.0 1.0
b_raw[2, 0] 0.570 0.305 0.101 1.193 0.007 0.007 1773.0 2025.0 1.0
b_raw[2, 1] 0.321 0.215 0.024 0.743 0.005 0.005 1879.0 2145.0 1.0
g_raw[0, 0] 1.187 0.389 0.453 1.915 0.012 0.007 1048.0 983.0 1.0
g_raw[0, 1] 1.127 0.372 0.457 1.859 0.011 0.007 1038.0 1049.0 1.0
g_raw[1, 0] 0.746 0.246 0.303 1.226 0.007 0.005 1056.0 957.0 1.0
g_raw[1, 1] 0.640 0.215 0.254 1.063 0.006 0.004 1092.0 1102.0 1.0
g_raw[2, 0] 0.569 0.202 0.202 0.955 0.006 0.003 1123.0 1105.0 1.0
g_raw[2, 1] 0.692 0.243 0.274 1.198 0.007 0.004 1128.0 1148.0 1.0
h_raw[0, 0] 0.981 0.359 0.372 1.716 0.011 0.006 1053.0 1225.0 1.0
h_raw[0, 1] 0.665 0.244 0.244 1.165 0.007 0.004 1056.0 1246.0 1.0
h_raw[1, 0] 0.769 0.304 0.251 1.373 0.009 0.006 1076.0 1308.0 1.0
h_raw[1, 1] 0.649 0.313 0.170 1.260 0.007 0.008 1423.0 1490.0 1.0
h_raw[2, 0] 0.941 0.369 0.295 1.657 0.010 0.006 1191.0 1458.0 1.0
h_raw[2, 1] 0.991 0.464 0.234 1.933 0.010 0.008 1952.0 2093.0 1.0
v_raw[0, 0] 0.975 0.597 0.077 2.158 0.008 0.010 3906.0 2311.0 1.0
v_raw[0, 1] 0.936 0.606 0.039 2.113 0.008 0.009 3781.0 2116.0 1.0
v_raw[1, 0] 0.646 0.598 0.000 1.819 0.014 0.009 1059.0 727.0 1.0
v_raw[1, 1] 0.755 0.603 0.001 1.946 0.010 0.009 2017.0 1373.0 1.0
v_raw[2, 0] 0.786 0.608 0.001 1.977 0.010 0.009 2269.0 1195.0 1.0
v_raw[2, 1] 0.780 0.602 0.001 1.962 0.009 0.009 2906.0 2006.0 1.0
c₁_raw[0, 0] 0.932 0.592 0.045 2.082 0.009 0.009 3525.0 2086.0 1.0
c₁_raw[0, 1] 0.927 0.598 0.031 2.074 0.008 0.009 3902.0 2410.0 1.0
c₁_raw[1, 0] 0.704 0.621 0.002 1.893 0.011 0.010 1953.0 1767.0 1.0
c₁_raw[1, 1] 0.822 0.581 0.006 1.919 0.009 0.009 3242.0 2062.0 1.0
c₁_raw[2, 0] 0.318 0.490 0.002 1.418 0.011 0.011 1553.0 3387.0 1.0
c₁_raw[2, 1] 0.799 0.600 0.009 2.003 0.008 0.009 3473.0 2772.0 1.0
c₂_raw[0, 0] 0.300 0.112 0.116 0.526 0.003 0.002 1364.0 1744.0 1.0
c₂_raw[0, 1] 0.503 0.187 0.186 0.869 0.005 0.004 1330.0 1477.0 1.0
c₂_raw[1, 0] 0.335 0.131 0.115 0.577 0.004 0.003 1304.0 2088.0 1.0
c₂_raw[1, 1] 0.917 0.332 0.341 1.555 0.009 0.006 1383.0 1902.0 1.0
c₂_raw[2, 0] 1.239 0.464 0.462 2.167 0.010 0.007 1947.0 2264.0 1.0
c₂_raw[2, 1] 1.351 0.469 0.523 2.266 0.012 0.008 1368.0 1682.0 1.0
Visualizing the curves#
Before plotting the curves, we have to generate predictions using the posterior.
# Create prediction dataframe
prediction_df = model.make_prediction_dataset(df=df, num_points=100)
# Use the model to predict on the prediction dataframe
predictive = model.predict(df=prediction_df, posterior=posterior)
This returns the posterior predictive distribution. We can use it to plot the estimated curves. Again, we specify the path where the generated PDF will be stored.
output_path = os.path.join(current_directory, "curves.pdf")
# Plot recruitment curves
model.plot_curves(
df=df,
prediction_df=prediction_df,
predictive=predictive,
posterior=posterior,
encoder=encoder,
output_path=output_path
)
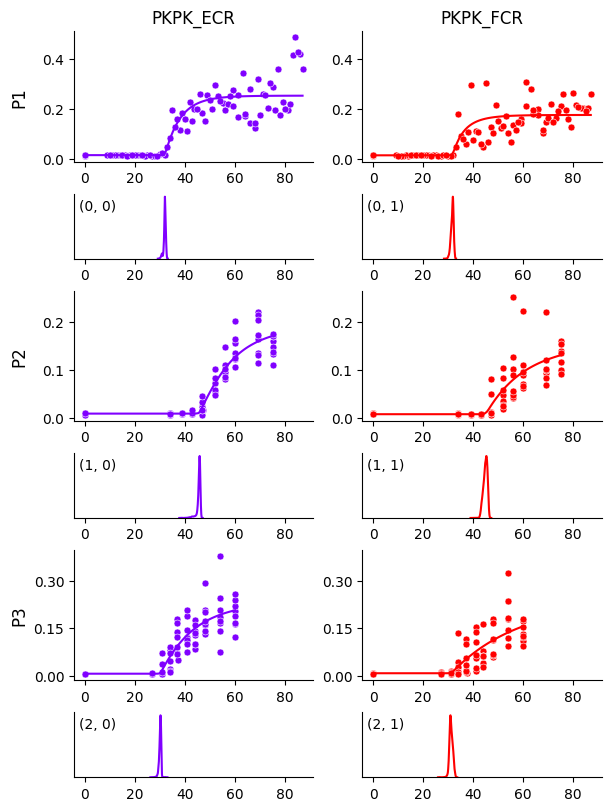
In each panel above, the top plot shows the estimated curve overlaid on data, and the bottom plot shows the posterior distribution of the threshold parameter.
Mixture extension#
The curves look good overall, except for participant P1 and muscle FCR, where the growth rate seems to be biased by a few data points. This can be addressed with a mixture model. To enable it, we can add the following line at the end of the model-building code:
# Enable mixture model
model.use_mixture = True
Accessing parameters#
Each participant, muscle combination is assigned a tuple index, which can be used to access the curve parameters, which are stored in the posterior dictionary as NumPy arrays.
Here we show how to access the threshold parameter.
from hbmep.util import site
# Threshold parameter
a = posterior[site.a]
Shape of a: (4000, 3, 2)
First dimension corresponds to the number of samples: 4000
Second dimension corresponds to the number of participants: 3
Last dimension corresponds to the number of muscles: 2
By default, we have 4000 posterior samples (4 chains, 1000 samples each). We can set more chains or samples by updating the model-building code:
# Use 10 chains, 2000 samples each, for a total of 20,000 samples
model.mcmc_params = {
"num_chains": 10,
"thinning": 1,
"num_warmup": 2000,
"num_samples": 2000,
}
The other curve parameters can be accessed similarly using their keys.
print(f"{site.b} controlds the growth rate")
print(f"{site.g} is the offset")
print(f"({site.g} + {site.h}) is the saturation")
b controlds the growth rate
g is the offset
(g + h) is the saturation
Saving the model#
We can save the model, posterior samples, and other objects using pickle for later analysis.
import pickle
# Save the model
output_path = os.path.join(current_directory, "model.pkl")
with open(output_path, "wb") as f:
pickle.dump((model,), f)
print(f"Saved model to {output_path}")
# Save the dataframe, encoder, and posterior samples
output_path = os.path.join(current_directory, "inference.pkl")
with open(output_path, "wb") as f:
pickle.dump((df, encoder, posterior,), f)
print(f"Saved samples to {output_path}")
# Save the MCMC object
output_path = os.path.join(model.build_dir, "mcmc.pkl")
with open(output_path, "wb") as f:
pickle.dump((mcmc,), f)
print(f"Saved MCMC object to {output_path}")
Using other functions#
Alternatively, we can use other functions to estimate the recruitment curves. The following choicej are available:
logistic-4, also known as the Boltzmann sigmoid, is the most common function used to estimate recruitment curves
logistic-5, is a more generalized version of logistic-4
rectified-linear
If estimating threshold is not important, we recommend using logistic-5 over logistic-4, which has a much better predictive performance.
For example, to use logistic-5 function, we need to update the model-building code and point to it, and rest of the tutorial remains the same.
# Set the function to logistic-5
model._model = model.logistic5